


Geralmente, representa-se os elementos de um conjunto por:
- Apresentação: Os elementos estão dentro de duas chaves.
A={a,e,i,o,u}
M={João,Maria,José}
-Descrição: É descrito por uma ou mais propriedades.
A={a: a é uma vogal}
N={x: x é um número natural}

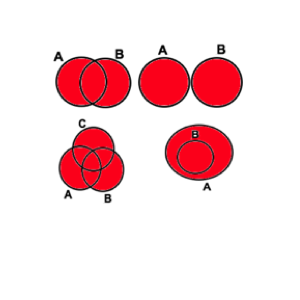
-Diagrama de Venn: Proposto por Jonh Venn(1834-1923), lógico inglês, são apresentados graficamente da seguinte forma:
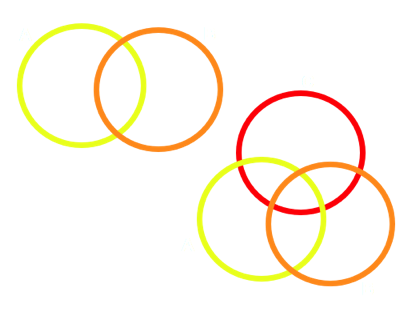

- Conjunto vazio: não possui elementos e é representado por { } ou Ø.
- Conjunto unitário: composto por 1 elemento.
Exemplos:
N = {b}
L = {l: satélite natural da terra} = {lua}
- Conjunto finito: possui um número finito de elementos.
Exemplo:
D = {1,2}
- Conjunto infinito: possui um número infinito de elementos.
Exemplos:
F = {1,2,3,4,...}
G = {...,1,2,3,4}
G = {...,1,2,3,4,...}
- Conjunto universo: usualmente representado pela letra U, contém todos os elementos relativamente ao espaço do qual se está a trabalhar.
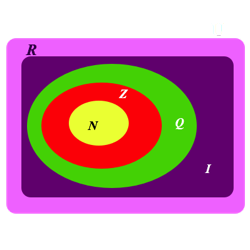
- Conjunto das partes de A ou conjunto potência: conjunto
de todos os subconjuntos de um conjunto A e denota-se por P(A) e é formado pelos subconjuntos:
- vazio.
- com um elemento.
- com dois elementos.
- ...
- com n -1 elementos.
- com n elementos.
- Exemplo:
-Cardinal de A: n(A)=3.
-Subconjuntos de A: Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}.
-Conjunto das partes de A : P(A)={Ø, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.
-Cardinal do conjunto das partes de A: n(P(A)) = 2n(A) = 23 = 8.

- A união de A e B é o conjunto de todos os elementos que pertencem ao conjunto A ou ao conjunto B.

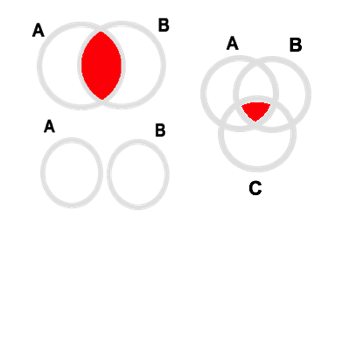
- A intersecção de A e B é o conjunto de todos os elementos que pertencem ao conjunto A e ao conjunto B.

- A diferença entre A e B é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.


- O complemento de B contido em A é a diferença entre os conjuntos A e B, ou seja, é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao conjunto B.
